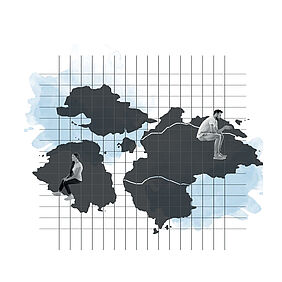
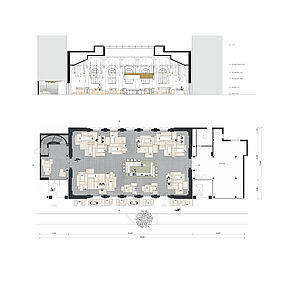
Als Inspirationsquelle des Entwurfs dient das oben genannte Zitat aus dem Werk „Peter Pan“ von J. M. Barries. Dies äußert sich nicht nur durch die kubischen Sitzlandschaften, die mit ihren unterschiedlichen Höhen Inseln auf einer Landkarte verkörpern. Auch die Bar, welche sich sowohl zent- ral im Raum befindet als auch in die Höhe ragt, nimmt dieses Thema auf. Durch ihre schweren Materialien (Fließen, Stein und Metall) steht sie wie ein Fels in der Brandung. So lässt sich die Bar als Festland interpretieren, von dem die umliegenden Sitz-Inseln ausgehen.
Eingangsbereich
Das Abenteuer der Protagonisten Peter und Wendy beginnt mit dem Flug ins Niemalsland über das Meer. In einer klaren Nacht weisen ihnen hierbei die Sterne am Himmelszelt den Weg. Um auch die Besucher auf die nächt- liche Reise Peter Pans mitzunehmen, ist der Eingangsbereich von dem Mo- tiv des Nachthimmels inspiriert. Neben den Lichtelementen an der Decke, findet sich außerdem das Element Wasser an den Wänden.
Raumbildungsprinzip - Module
Die Systemgastronomie ist organisatorisch von standardisierten und vereinheitlichten Strukturen geprägt und unterscheidet sich damit von der Individualgastronomie. Dieser Gedanke wurde im vor-
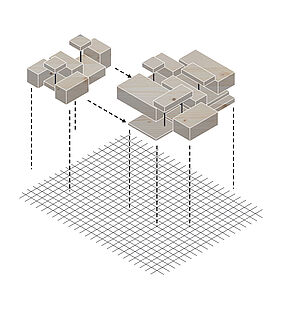
liegenden Entwurf bedacht. Um eine typische Expansion und den damit verbundene Bau eines weiteren Restaurants zu erleichtern, kann stets nach demselben Prinzip vorgegangen werden: zunächst
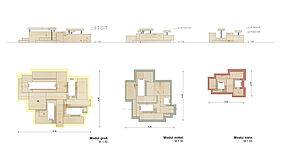
wird ein 30cm x 30cm-Raster über den Grundriss gelegt, auf wel- chem die drei verschiedenen Module – klein, mittel, groß – verteilt werden. Durch das Drehen der jeweiligen Module entsteht, trotz der einfachen Vervielfältigung, jedes Mal ein spannendes und dennoch individuelles Gesamtbild. Dies wird dadurch erleichter, dass die Mo- dule vorrätig produziert werden können und diese somit jeder Zeit unkompliziert einsetzbar sind.
Logo
Das Logo des Restaurants ist angelehnt an die markanten kubischen Formen, welche auch im präsentierten Entwurf den Raum maßgeblich bestimmen und charakterisieren. Im zweidimensionalen Bereich tritt das Logo in Form einer Isometrie auf, während im dreidimensionalen Raum damit gespielt wird und die Achsen zu echten Kanten werden.